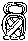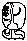Sistemele calendaristice folosite în lumea antică reflectă nevoile agricole, politice și rituale caracteristice societăților în care au înflorit. Observațiile astronomice pentru stabilirea solstițiilor de iarnă și de vară au fost utilizate în urmă cu trei până la patru milenii. Până în secolul al XIV-lea î.Hr., chinezii Shang stabiliseră anul solar ca fiind de 365,25 zile și luna având 29,5 zile. Calendarul lunisolar, în care luna ritualică se bazează pe Lună și anul agricol pe Soare, a fost folosit în întregul Orient Apropiat antic (cu excepția Egiptului) și a Greciei din mileniul III î.Hr. Calendarele timpurii erau împărțite fie în treisprezece luni lunare de 28 de zile, fie în douăsprezece luni lunare alternative de 29 și 30 de zile și mijloace întâmplătoare pentru a reconcilia anul lunar de 354/364 de zile cu anul solar de 365 de zile.
Studiul sistemelor calendaristice istorice și moderne este o aventură fascinantă care implică interconectarea agendelor politice, religioase și economice. Următoarea discuție despre calendarul Mayaș se bazează pe istoria cuprinzătoare a civilizației maiașe. Înainte de a începe, trebuie să precizăm că termenul Mayaș este folosit de istorici atât ca substantiv, cât și ca adjectiv pentru a se referi la oameni, cultura și artefactele lor. Cu toate acestea, există multe limbi înrudite ale mayașilor; prin urmare, istoricii folosesc termenul Mayaș pentru a se referi la familia de limbi Mayașe, atât ca substantiv, cât și ca adjectiv.
Civilizația Mayașă din sudul Mexicului, Guatemala și Belize s-a dezvoltat în secolele IV-X e.n. Au fost astronomi desăvârșiți și au creat un sistem de calendar fascinant. Ei au folosit un sistem de numere vigesimal (în bază 20), inclusiv conceptul de zero, cu mult înainte ca europenii să elimine numerologia romană. Sistemul Mayaș folosește doar trei simboluri pentru zero (un glif în formă de coajă), unul (un punct) și cinci (o bară) pentru a reprezenta unități de la zero la 19. De exemplu, numărul 13 a fost reprezentat ca trei puncte și două bare . S-a folosit o notație pozițională în care fiecare poziție vigetă reprezintă zilele în puteri crescătoare de 20, cu excepția celei de-a doua poziții (luni), unde radixul este 18 în loc de 20. Acest sistem a fost folosit pentru a reprezenta atât datele absolute ale evenimentelor proeminente, cum ar fi cuceriri, ascendențe și așa mai departe și date relative.
Calendarul Maiaș
Calendarul pentru Numărătoarea Lungă, Calendarul Tzolkin și Haab
Calendarul Mayaș este un sistem de trei calendare și almanahuri care se întrepătrund, care a fost folosit de mai multe culturi din America Centrală, dintre care cea mai cunoscută este civilizația Mayașă. Cu toate acestea, nu este o invenție mayașă. Calendarul mayaș datează cel puțin din secolul al V-lea î.Hr. și este încă în uz în unele comunități mayașe și astăzi. Cu toate acestea, chiar dacă mayașii au contribuit la dezvoltarea ulterioară a calendarului, ei nu l-au inventat de fapt. Același sistem a fost folosit de majoritatea culturilor din America Centrală pre-columbiană, inclusiv de cele care precedau Mayașii.
Calendarul Mayaș constă din trei calendare corespunzătoare separate: Calendarul pentru Numărătoarea lungă, Calendarul Tzolkin (calendarul divin) și Haab (calendarul civil). Fiecare dintre ele este ciclic, ceea ce înseamnă că trebuie să apară un anumit număr de zile înainte ca un nou ciclu să poată începe.
Cele trei calendare sunt folosite simultan. Tzolkin și Haab identifică zilele, dar nu și anii. Data Numărării lungi vine mai întâi, apoi data Tzolkin și ultima apare data Haab. O dată tipic mayașă s-ar citi: 13.0.0.0.0 4 Ahau 8 Kumku, unde 13.0.0.0.0 este data Numărării lungi, 4 Ahau este data Tzolkin și 8 Kumku este data Haab.
Civilizația Maiașă folosea de fapt două calendare, pentru un an sacru de 260 de zile și pentru un an vag de 365 de zile. Alături de alte popoare mezoamericane, mayașii folosesc anul sacru în scopuri religioase și pentru a numi copii, de exemplu. Anul vag este folosit pentru lucruri precum plantarea culturilor. Cel mai mic multiplu comun dintre cele două calendare, numit runda calendaristică, are 18.980 de zile sau 73 de ani sacri sau 52 de ani vagi. O lună sau uinal în calendarul Mayaș, constă din 20 de zile solare sau rude. Anul sacru de 260 de zile sau tzolkin constă din 13 luni a 20 de zile, în timp ce anul vag de 365 de zile sau haab, constă din 18 luni a 20 de zile, numite tun, urmate de o „lună” intercalară de cinci zile numită uayeb.
Data este identificată în continuare prin numărarea zilelor, de la „data creării”, folosind calendarul Număr lung. O dată tipică de numărare lungă are următorul format: Baktun.Katun.Tun.Uinal.Kin.
Kin = 1 zi.
Uinal = 20 kin = 20 de zile.
Tun = 18 uinal = 360 zile.
Katun = 20 tun = 360 uinal = 7.200 zile.
Baktun = 20 katun = 400 tun = 7.200 uinal = 144.000 zile.
Ciclurile mai lungi pot fi încorporate în calendarul Mayaș. Un katun este format din 20 de tun-uri (aproximativ 19,7 ani), un baktun din 20 de katun (aproximativ 395 de ani), un pictun din 20 de baktun (aproximativ 78,9 secole), un calabtun din 20 de pictun (aproximativ 158 de milenii) și un kinchiltun din 20 calabtuns (aproximativ 3,16 milioane de ani). Există dovezi care sugerează că mayașii erau conștienți de faptul că anul vag diferă ușor de anul solar real, dar nu există dovezi că au făcut ceva în acest sens.
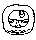
În calendarul Mayaș zilele fie ale anului sacru, fie ale anului vag sunt reprezentate prin digrafe viget-glife articulate similare cu figura din stânga. Viget-ul deschis din stânga figurii codifică 14 așa cum este descris mai sus. Gliful din dreapta, numit gliful zilei, codifică un viget vag în funcție de fața sa.
O dată calendaristică mayașă este formată din două digrafe reprezentând ziua anului sacru urmată de ziua anului vag. Când este necesar, în calendarul mayaș anii sunt reprezentați în notație pozițională, unde fiecare viget deschis reprezintă un coeficient și viget opac multiplicatorul pozițional sau gliful anului. Formatul variază oarecum în funcție de stilul calendarului, cu vigetul deschis plasat în partea de sus sau în stânga ca în figură, care este tradus literal 14 Pictun (aproximativ 103 secole).
Vino să vezi LIVE!
Vom studia împreună mandala personală și căile prin care putem accesa potențialul divin, drumul și misiunea personală, prin intermediul Calendarului Mayas Tzolkin

Zilele și Lunile în Calendarul Mayaș
Istoricii numără anul sacru în numerele lunii de la 1 la 13 și glife ale zilei corespunzătoare numerelor de la 1 la 20. În acest format nu există glife ale lunii. Numerele, glifele și numele zilelor din calendarul Mayaș, sunt:
| Ziua | Glifa | Numele | Ziua | Glifa | Numele | Ziua | Glifa | Numele | Ziua | Glifa | Numele |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Imix | 6 | Cimi | 11 | Chuen | 16 | Cib | ||||
| 2 | Ik | 7 | Manik | 12 | Eb | 17 | Caban | ||||
| 3 | Akbal | 8 | Lamat | 13 | Ben | 18 | Etznab | ||||
| 4 | Kan | 9 | Muluk | 14 | Ix | 19 | Cauac | ||||
| 5 | Chicchan | 10 | Oc | 15 | Men | 20 | Ahau |
Fiecare zi următoare face ca atât numărul zilei, cât și numărul glifului să avanseze cu unu, de exemplu, 1 Imix, 2 Ik, …, 13 Ben, 1 Ix, 2 Men și așa mai departe. Deoarece 13 și 20 nu au divizori comuni, acest sistem reprezintă în mod unic toate cele 260 de zile ale anului sacru calendaristic mayaș.
Istoricii numără anul vag în numerele zilei de la zero la 19 și glife ale lunii corespunzătoare numerelor de la unu la 19, unde ultima lună reprezintă cele cinci zile nenumărate ale haab. Numerele, glifele și numele lunii din calendarul Mayaș, sunt:
| Luna | Glifa | Numele | Luna | Glifa | Numele | Luna | Glifa | Numele | Luna | Glifa | Numele |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Pop | 6 | Xul | 11 | Zac | 16 | Pax | ||||
| 2 | Uo | 7 | Yaxkin | 12 | Ceh | 17 | Kayab | ||||
| 3 | Zip | 8 | Mol | 13 | Mac | 18 | Cumku | ||||
| 4 | Zotz | 9 | Chen | 14 | Kankin | 19 | Uayeb | ||||
| 5 | Tzec | 10 | Yax | 15 | Muan |
Fiecare zi următoare face ca numărul zilei să avanseze cu unu. Când numărul zilei se încadrează de la 19 la zero (sau în luna uayeb de la 4 la zero), gliful lunii avansează cu unu. De exemplu, o zi Mayașă scrisă 0 (zero) Pop este urmată de 1 Pop, …, 19 Pop, 0 Uo, 1 Uo și așa mai departe. O dată rundă calendaristică mayașă constă din ziua sacră concatenată cu ziua vagă, de exemplu, 2 Yaxin 10 Ahau. O combinație unică de zi sacră și zi vagă se repetă o singură dată în runda din calendarul Mayaș, unde începutul fiecărei runde este stabilit la corespondența 2 Ik 0 Pop.
Runda calendarului mayaș și datele de numărare lungă
Istoricii ce au deslușit calendarul Mayaș, scriu o dată rotundă calendaristică de numărare lungă sub forma, de exemplu, 9.17.0.0.0 13 Ahau 18 Cumku, unde primele cinci câmpuri viget desemnează baktuns, katuns, tuns, uinals și kins în ordine. Următorul digraf desemnează ziua sacră a rundei calendaristice, iar ultimul digraf este ziua vagă. Mayașii au gravat date lungi de numărare pe monumente de piatră numite stellae ca 15 digrafe citite de sus în jos. În partea de sus este o variantă a glifului alautun. Chiar sub acestea sunt cinci digrafe reprezentând în calendarul Mayaș, numărul de baktuns, katuns, tuns, uinals și kins, așa cum se arată mai jos:
| Anii | Viget | Glifa | Numele |
|---|---|---|---|
| 3,1 mega ani | Long Count | ||
| 158 secole | 9 | Baktun | |
| 7,9 secole | 17 | 
| Katun |
| 394 ani | 0 | 
| Tun |
| 19,7 ani | 0 | Uinal | |
| ani | 0 | 
| Kin |
| ziua sacră | 13 | 
| Ahau |
| … | |||
| ziua vagă | 18 | 
| Cumku |
Alte gravuri ce aparțin calendarului Maya, includ:
kinchiltune
calabtune

pictune

Următorul digraf reprezintă ziua sacră și, după niște glife intermediare, ultimul dintre cele 15 digrafe reprezintă ziua vagă.
Calendarele Mayaș și Gregorian
Un punct de interes istoric considerabil este concilierea calendarelor mayaș și gregorian. Aceasta înseamnă
- selectarea unei origini pentru numărarea lungă inițială,
- selectarea rundei calendaristice corespunzătoare acelei numărări și
- corelarea unei anumite date de numărare lungă din calendarul Maya cu data corespunzătoare din Calendar gregorian.
Mayașii și-au calculat cronologia în mari cicluri de 13 baktuns (aproximativ 5.128 de ani solari), cu începutul ciclului actual 13.0.0.0.0 4 Ahau 8 Cumku corespunzând unei zile în 3114 î.Hr. Aceasta stabilește relația dintre numărarea lungă și numerotarea rundei calendaristice.
Corelația general agreată între calendarele gregorian și maya este corelația Goodman-Martinez-Thompson (GMT), care plasează katunul de numărare lungă care se termină 11.16.0.0.0 13 Ahau 8 Xul la 14 noiembrie 1539 (gregorian). Deși GMT este convenabil pentru calculele calendaristice, trebuie remarcat faptul că calendarul gregorian în sine există doar din 15 octombrie 1582, așa cum a proclamat Papa Grigore al XIII-lea [4]. Este un exercițiu interesant, dar complicat, de a construi programe de calcul care convertesc între calendarele gregoriane și maya. De exemplu, pentru 14 august 1995, programul de calcul Excel afișează Ziua Iuliană modificată 49943 și data de numărare lungă Maya 12.19.2.7.0 8 Ahau 8 Uo.

Te așteptăm în București la …
ATELIERUL EDUCAȚIONAL DESPRE FLOAREA VIEȚII ESTE STRUCTURAT ÎN 4 PĂRȚI PRINCIPALE:
Partea 1 – Despre Floarea Vietii
Partea 2 – Mandala personala
Partea 3 – Studierea semnului și tonului sub care v-ați născut în calendarul mayaș Tzolkin
Partea 4 – Despre beneficiile Ogonului
Vom putea discuta și răspunde la întrebările publicului, după prezentare.
Bibliografie despre calendarul mayaș și cel gregorian
- Calendar. Enciclopedia Britannica Macropaedia, ed. a XV-a, vol. 15, p. 460-477. Encyclopaedia Britannica Co., New York, NY, 1986.
- Dershowitz, N. și E.M. Reingold. Calcule calendaristice. Software Practice and Experience 20, 9 (septembrie 1990), 899-928.
- Mills, D.L. Despre cronologia și metrologia scalelor de timp ale rețelei de calculatoare și aplicarea acestora la Network Time Protocol. ACM Computer Communications Review 21, 5 (octombrie 1991), 8-17. Prezentare PostScript
- Moyer, G. Calendarul gregorian. Scientific American 246, 5 (mai 1982), 144-152.
- Morley, S.G., G.W. Brainerd și R.J. Distribuitor. The Ancient Maya, ed. a 4-a. Stanford University Press, Stanford, CA, 1983.